Ecrire les nombres rationnels suivants en utilisant des nombres entières inférieures à 12 dans le numérateur et le dénominateur.
On va corriger un exercice qui concerne les nombres rationnels introduction pour le niveau maths 3éme, écrire les nombres
rationnels suivants en utilisant des nombres entiers inférieurs à 12 dans le
numérateur et dans le dénominateur, on va convertir ces nombres rationnels à
des nombres rationnels tel que le numérateur sera un nombre entière inférieur à 12 et le dénominateur devient aussi un nombre
entière inférieur à 12.$ads={1}
5,5 divise par 3,3 on va décomposer le numérateur 5,5 = 5 × 1,1 et on va aussi décomposer le dénominateur 3,3 = 3 × 1,1 dans ce cas on a un facteur commun 1,1 entre le numérateur et le dénominateur, on peut supprimer le facteur commun et on écrit le reste 5 divise par 3 donc on à obtenir un nombre rationnel tel que le numérateur 5 est un nombre entière inférieure à 12 et le dénominateur 3 est un nombre entière inférieure à 12.
125 divise par 25 pour trouver un nombre rationnel tel que le numérateur et le dénominateur devient des nombres entières inférieures à 12 on va décomposer 125 = 5 × 25 et on va décomposer 25 = 1 × 25, vous observez que 25 se trouve dans le numérateur et le dénominateur, on peut simplifier le résultat, on va supprimer le facteur commun 25 dans le numérateur et dans le dénominateur, et on garde le reste 5 divise par 1 est égal 5.
28 divise par 35 toujours on va décomposer le numérateur et le dénominateur, 28 est égal le produit de deux facteurs 4 × 7 et 35 est égal le produit de deux facteurs 5 × 7 maintenant on obtient un facteur commun 7 on peut supprimer le facteur commun entre le numérateur et le dénominateur et on écrit le reste 4 divise par 5 donc on a obtenir un nombre rationnel tel que le numérateur et le dénominateur sont des nombres entières inférieur à 12.


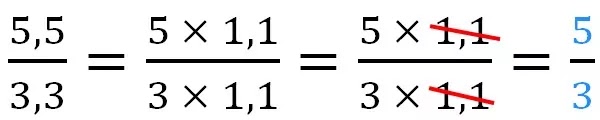
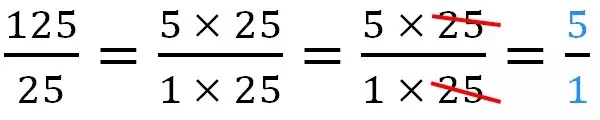
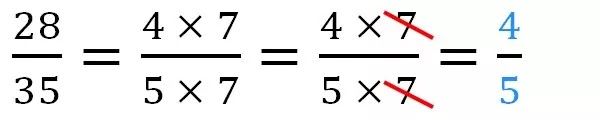
Enregistrer un commentaire